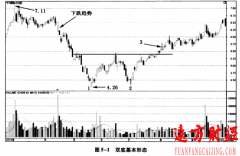
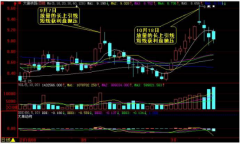
股市心理学37:多元系统
在接受了众多的教育后,人们往往会发现,自己所面对的问题,原来只需要有限 的选择,甚至两种不同的选择,即二元论与三元论的观点,便能够得以解决。而现实 生活中的大部分情形,包括股票市场,则应该用多值论的观点来处理它们。一位赌徒 既可能一夜暴富,也可能瞬间破产。而一位明智的观察者则很可能将赌注分散在不同 的篮子里,并同时投资一部分保值债券和采用多样化的战略和战术。
自此,你或许已经十分清楚,人们能够采用多种多样的方法来解决问题。当 我们说到一元论的方法时,我们立刻能够找出许多一元论适用的情况。例如,当 你在后退的过程中拌倒的时候,你的第一个反应便是设法抓住周围的栏杆,这似 乎就是唯一合理的急救措施。同样,也有许多二元论适用的场合,在这样的情况 下,你将拥有两种可能的行动措施,如果社会势力并不阻碍或个人价值观并不禁 止这两种行为,你将有两种不同的选择。你有权接受实会的邀请,也完全可以拒 绝参加宴会。三元论的情形也随处可见:你既可以拥护共和党,也可以为民主党 投上一票,或者干脆待在家里,对谁都不闻不问4
当然,在某些地方,投票选举的方案并不止于在两个政党中挑选其中一个, 或是千脆弃权。例如,在法国,提名竞选的政党往往高达半打,甚至一打之多。 于是,人们便有了众多的选择。
然而,人们往往忘却了他们拥有众多选择的事实。他们忽视那些唾手可得的 机会,就像忽略门厅的那头大象一样。比如,乔或许觉得,其实有一半的原因是 出于承诺,自己必须对得起玛莉,所以必须和她结婚。他或许忘了,或是忽略了,或是干脆拒绝承认自己还有娶玛莉和不娶玛莉两种可能的抉择(二元论的观点, “不是/就是”的两种情形)。他也不会给予自己选择娶玛莉、或是娶琼,或是根本 不结婚(三元论的说法)的机会。而你也不必指望一个沉溺爱河的多情郎,还有 空闲去考虑自己婚姻的多种选择:娶玛莉,或是娶另外十个姑娘中的一位,或是 根本不谈及婚嫁(多元理论的观点)。
一位采用多元化战略的賭徒也不必走入彻底破产的境地。赌博游戏的结局也 将多于一夜暴富或是瞬间破产的两种命运。你既可以下注1美元,也可以投入 5美元,或是100美元,甚至1 〇〇〇美元,你有多种多样的选择。当然,正如你所 知道的,许多玩牌的赌徒,从来只给自己两个行动的选择:孤注一掷,或是干脆 放弃。
很难相信,人们限制自己选择机会的冲动竞是如此的强烈。例如,大多数商 品交易商,似乎都青睐于某种单一商品即所谓的“最佳商品”的买卖,在他们眼 中,似乎只有对某种单一商品的忠诚才有可能得到最令人满意的结果。他们总是 强烈地反对这样的建议,即把资金分散和经营多种商品的做法,他们从不考虑当 某个商品的合同不利于自己的时候,分散投资的方法够避免遭受全面损失等的好 处。他们并不需要多元的选择,而是希望把所有的情况都简化为“不是/就是”的 简单情形,并在最终分析和决策的时候,排除其中一个“不好”的选择,剩下唯 一一个毫无灵活性可言的抉择。
事实上,我们所生活的世界,充满着各种各样的多元选择的情形。例如,一本 电话簿,就是一个多元选择的目录,我们可以从中选出成千上万个不同的电话号 码。自动电梯的指示器也有多个显示值,尽管你的选择将局限于你所需到达的楼 层所指示的整数值(一般来讲,你不可能按下4V3的指示器),此外,你的选择还受 到大楼楼层数目的局限,指示值中很可能还包括两个负值,它们分别指代地下一 层和地下二层。许多自动报聱装置,也被设计为多元系统,它提供多个启动时间, 比如,每隔15分钟启动一次。对于这样的定时器,你可以利用它,将收音机的播 放时间自动地设置为7:00, 7:15,以及7:30等,而不是7:03以及7:16等。
股票的价格,也属于多元系统。如果股票的报价以"8为一个变动单位的话, 那么,股票的每一次上涨或下跌的幅度将不可能少于1/8个单位。在研究圆周几何 的时候,我们知道,通过不断地增加圆的内切正多边形或外切正多边形的边数, 我们最终得到的正多边形的形状及其边长,也将不断地接近圆本身,因此,我们 可以说,圆的内切正多边形或外切正多边形边长的极限值将是圆周本身。当然, 我们实际上也不可能画出无穷边数的多边形,但是,当多边形的边数增加到足够多的时候,我们所得到的图形也将十分接近我们所希望的形状了。
生活中,许多时候拥有多个参考的视角或思考的角度,而不是局限于一种、 两种或三种简单极端的选择,对我们的人生来说具有十分重要的意义。很多时候, 我们在图形上、地图上,或是我们的评价系统中,设置的基准点越多,我们所画 出的图形也越能够精确地描述它所代表的外界客观事实,而基于这幅图形所得出 的结论也将具有与客观实际更好的一致性。不用多费口舌,我们也会明白,一幅 地图,越接近它所代表的客观事实,对我们实现目标的愿望将越有帮助。